DFS로 풀게되면 시간초과의 우려가 있어 DP로 풀었다.
현재칸을 ( i, j )라고 했을 때,
( i, j-1 ) 의 칸에서 이어지는 경우,
( i-1, j ) 의 칸에서 이어지는 경우,
( i-1, j-1 ) 의 칸에서 이어지는 경우 3가지의 경우로 파이프가 이어질 수 있다.
3차원배열을 선언하여 각 칸에 들어오는 파이프의 개수가
가로에서 들어왔는지, 세로에서 들어왔는지, 대각선에서 들어왔는지 개수를 세주었다.
index => 가로 : 0 대각선 : 1 세로 : 2
각 그림에서 주황색 칸은 값을 채우려는 현재 위치이고
빨간색 화살표는 파이프가 이어지는 방향,
파란색 화살표는 이으려는 파이프의 이전 파이프의 방향이다.
1. ( i, j-1 ) 칸의 경우 가로로 이어지는 경우 dp[0][i][j] = dp[0][i][j-1] + dp[1][i-1][j-1]

2. ( i-1, j-1 ) 칸의 경우 대각선으로 이어지는 경우 dp[1][i][j] = dp[0][i -1][j-1] + dp[1][i-1][j-1] + dp[2][i-1][j-1]

3. ( i-1, j ) 칸의 경우 세로로 이어지는 경우 dp[2][i][j] = dp[1][i -1][j] + dp[2][i-1][j]
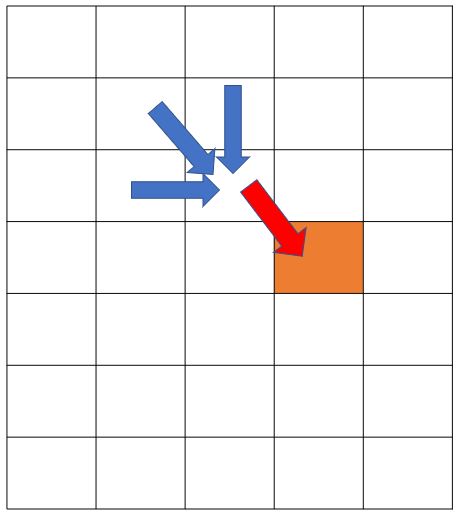
3차원 배열에서 ( n,n ) 칸에 있는 수의 합이 파이프를 이을 수 있는 모든 경우의 수이다.
하지만 문제에서 중간중간 벽을 놔버린다.
가로와 세로의 경우 벽이 있는 부분을 안세버리면 그만이지만
대각선의 경우는 조금 고려사항이 있다.
**
대각선의 경우는 놓으려는 칸 왼쪽, 대각선, 위쪽 모두 칸을 차지해버리므로
만약 위쪽칸이나 왼쪽칸에 벽이 놓여져있다면 합산을 해주면 안된다.
**
'Algorithm' 카테고리의 다른 글
| 백준 - 1422번(숫자의 신) / C++ (0) | 2021.02.22 |
|---|---|
| 프로그래머스 - 가장 큰 수 / C++ (0) | 2021.02.22 |
| 프로그래머스 - Summer/Winter Coding(2019)(멀쩡한 사각형) / C++ (0) | 2020.10.28 |
| 백준 - 15686번(치킨 배달) / C++ (0) | 2020.07.09 |
| 백준 - 15685번(드래곤 커브) / C++ (0) | 2020.07.09 |